Things I wonder about

This is a short list of speculations about physics.

1) Can quantum mechanics be derived from classical physics with CTCs? There are hints that this is the case. In 2008, Aaronson and Watrous found that with CTCs both classical and quantum computers can solve PSPACE problems (arXiv.0808.2669v1) http://arxiv.org/abs/0808.2669. Quantum mechanics needs to be weaker than this so the CTCs in our universe that give rise to QM must be far away and/or randomized to hide most of the computational power CTCs give us. Perhaps quantum eigenstates are fixed points of whatever broken CTC we are in and the exponential dimensions of Hilbert space are needed to keep track of all possible paradoxes created by the CTC. Any classical explanation of QM requires internal epistemically limited observers that can only see a small part of the system.

2) Is spacetime dimension more like a taking a power or tetration? Our normal intuition is that computational complexity is only polynomial in spacetime dimension. However, I suspect that introducing conformal symmetry or closed timelike curves make adding a dimension like the powerset operation. Spacetime complexity should be O(^Dn), where the superscript D represents the level of tetration. Computational complexity should work out to be (D-2)-EXPSPACE or (D-1)-EXPTIME depending on the ability of physics to generate space for computation. The question is whether a computer can generate both exponential space and time on the fly or whether it can only generate exponential time directly. A CTC based argument would suggest that only (D-2)-EXPSPACE is needed to avoid paradoxes, but from a conformal perspective it seems like there could exist a method expand space complexity as much as time complexity so we can solve (D-1)-EXPTIME problems. Either complexity class would still mean spacetime complexity grows like tetration and both give us such extraordinary computational power that all problems we have seriously considered (except things like formal verification of higher-order pushdown automata) would become trivial. Perhaps the most obvious difference is that if we have (D-2)-EXPSPACE cryptography will be similar , while with (D-1)-EXPTIME cryptography would work as in P assuming that P != NP and (D-1)-EXPTIME != N(D-1)-EXPTIME.

This tetrational growth in spacetime complexity would mean that quantum gravity requires a much larger ((D-1)-EXP dimensional) Hilbert space in order to quantize a D dimensional manifold. Quantization with a smaller Hilbert space might produce non-unitary nonlinear evolution. Perhaps this is why quantum physics near black holes shows signs of being non-unitary. Two dimensional objects like strings would be the highest dimensional objects with an ordinary size Hilbert space. This would be the reason that 3 dimensional manifolds are so hard to quantize.

3) There appears to be a deep connection between the number of involutions in the symmetric group (http://en.wikipedia.org/wiki/Telephone_number_(mathematics) and http://oeis.org/A000085) and dimensions in string theory. The involution numbers corresponding to S₂ through S₅ are< 2, 4, 10, 26. These are the dimensions of the string, the four dimensions we observe, the ten dimensions of superstring theory, and the 26 dimensions of bosonic string theory. The connection is not just with string theory but also with exceptional groups, unimodular lattices, and perhaps Galois theory. Why is that? Is there a string theory lurking in 76 dimensions?

4) Is there a string theory with critical dimension D=4? We live in a universe with four observable dimensions, four dimensions seems to have nice properties and it is the involution number for S₃. It would almost certainly be easier to test string theory if we knew how and why it generates a four dimensional universe. If a critical string theory exists in four dimensions what would it look like? We get 10D superstring theory by adding fermions and supersymmetry and compactifying the remaining 26D bosons to 10D. Perhaps a new kind of field and a new symmetry on top of supersymmetry would require its string theory to exist in four dimensions. My guess is that this new kind of field would carry extrinsic angular momentum and the new symmetry would transform rotating particles to fermions and bosons.

Nonlinear Quantum Mechanics, NP and the Polynomial Hierarchy

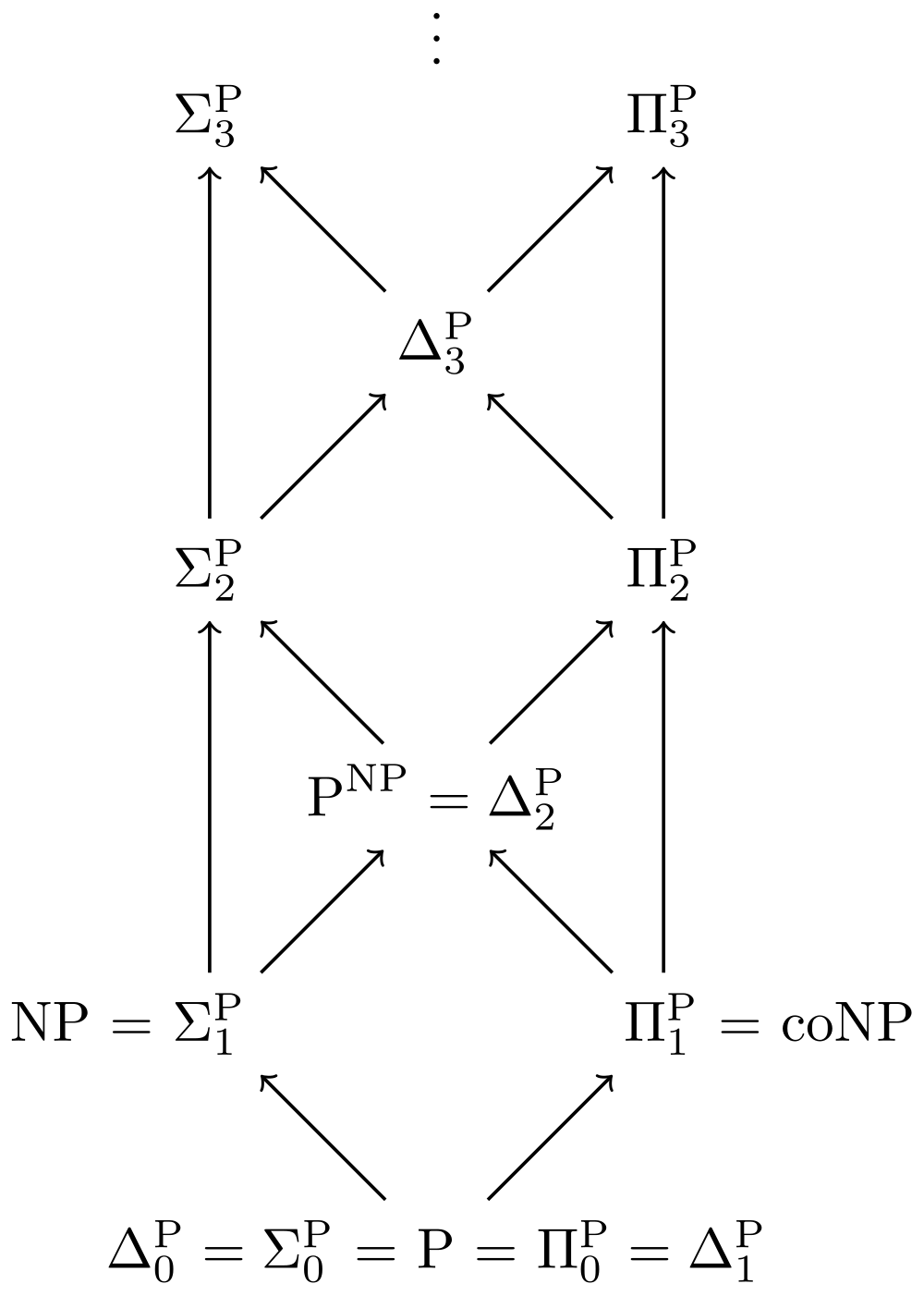
I've been reading Scott Aaronson's Quantum Computing since Democritus and he makes a point that "physicist complexity classes" should be closed under oracle calls to themselves. That is, PCC^PCC = PCC for any complexity class PCC which is equivalent to the computational power of some laws of physics. This is because the physics should include oracle calls to other computer built with the same physics. What does this mean for nonlinear QM? We know NP and coNP are contained in BNLQP (Bounded-Error Nonlinear Quantum Polynomial-Time). So that NP^NP  is contained in BNLQP^BNLQP = BNLQP and in this way the entire polynomial hierarchy is contained inside BNLQP. Just how big is BNLQP?  The physically reasonable complexity class argument would mean $latex PH \subseteq BNLQP $ If NP is strictly contained in BNLQP, can we find reasonable laws of physics such that a computer built with those physics can solve NP (and nothing more) in polynomial time? Then, using physical reasoning we could prove that NP^NP=NP=PH=coNP. If we prove NP \neq

Polynomial Hierarchy on Wikipedia